![]()
Lecture Topic:
Homogeneous Coordinate Transforms (HCT) in 2D
so far we have see that translation, scaling and rotation are:
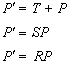
In order to make translation into a multiplication (like scaling and rotation) we introduce homogeneous coordinates.
With HC's we used Tuples in 2D; (x,y,w) also one of the coordinates must be non-zero (typically w is non-zero).
if
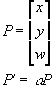
then P' and P represent the same point....
the Cartesian coordinates of the homogeneous point are:
(x/w,y/w,1)
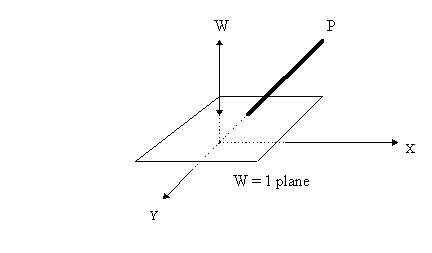
The XYW homogeneous coordinate space, with the w=1 plane and point P(x,y,w) projects onto the w=1 plane.
Tuple multiplies require 3x3 transforms (i.e., homogeneous coordinate transformations in 2 space require a 3x3multiple). Note, if all you want to do is translate, you are doing 3 multiplies and 2 adds for nothing!
The matrix form for the translation is:
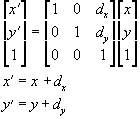
But the multiplication by 0 takes the computer as long to do as the multiplication by a non-zero(unless we intercept this special case).
Note: some graphics text books premultiply rather than postmultiply by the column vectors. To convert between the forms, used transposition:
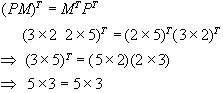
You should know how to do this! Try it for homework.
suppose we let
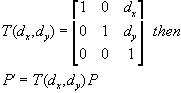
Now that we can perform the HCT's using the matrix multiplications, we can concatenate many transformations into a single matrix representation.
![]()
This is a concatenation of two transformations, which are equivalent to:
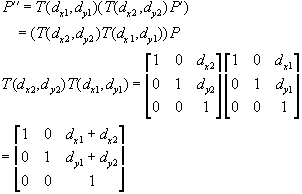
The matrix product is also called compounding, catenation, concatenation or composition.
Once the transform is formulated, it may be applied to all points in the scene.
Several policy issues must be resolved in order to implement matrix compounding:
All this applies to scaling too, for example:
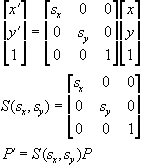
successive scalings are multiplicative:
![]()
Back substÆng:
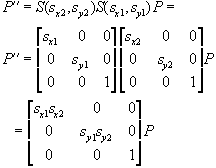
Now we can use a shorthand to describe the rotation matrix:
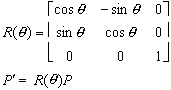
For HW, show successive rotations are additive.
Note that the 2x2 in the upper left or the rot matrix,
![]() has two rows (and columns )
has two rows (and columns )
The following special orthogonal properties hold for the rotation matrix:
1. Each is a unit vector
2. each is perpendicular to the other (dot product is zero)
3. The first and second vectors will be rotated to lie on the positive x and y axes.
The rotation and translation are rigid-body transformations since they do not distort the object.
scale, however, is not a rigid body transformation:
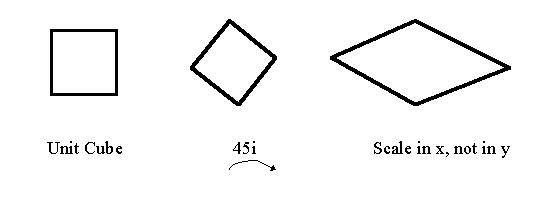
affine transformations consst of sequences of rotation, translation, scale operations as well as shear. They preserve parallelism of lines, but not lengths or angles.
Shear can go in the x and or y direction. For example:
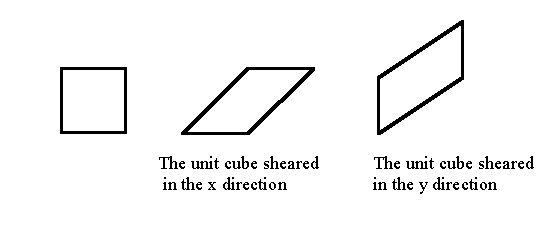
The shear matrices in the x and y direction are:
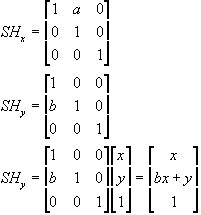
Composition of 2D transformations
By composing a single transformation matrix, we can perform all affine transforms in a single matrix multiply.
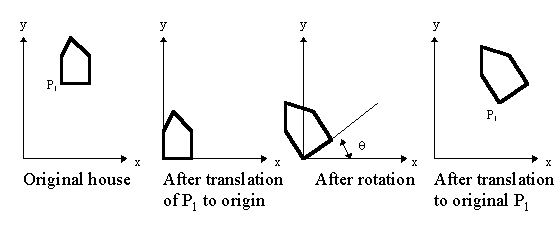
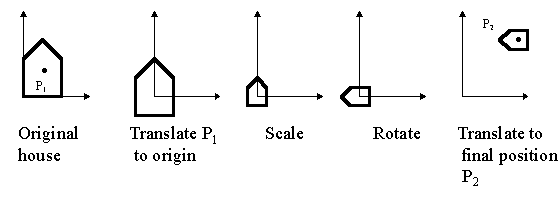
To rotate a point about P1:
1. translate so that P1 is at the origin
2. rotate
3. translate back
For example:
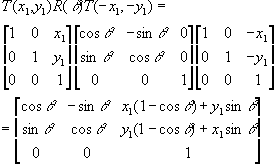
For scaling:
And for scale, rotate and position:
![]()
In general, matrix multiplication is not commutative.
Window to viewport transformation
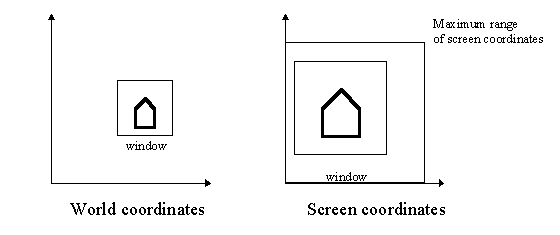
World-coordinates may be floating point coordinates which make use of whatever units are meaningful to the problem. This comes expensive, however, since floating point computations can slow us down....still we may be forced to keep them. Some people use infinite precision computations in order to keep geometries consistent. This is even more expensive, but may be worth the trouble.
Using world-coordinates you may define a rectangle called world-coordinate window this maps to a screen coordinate entity called the viewport.
If the world-coordinate window and viewport do not have the same aspect ratio a scaling occurs (more computation).
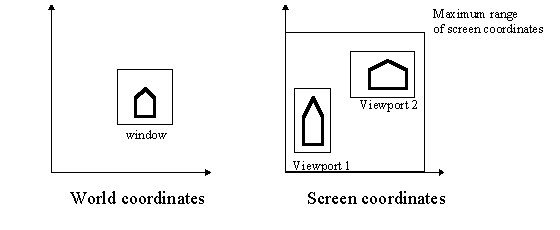
Effect of drawing output primitives with two view ports.
import java.applet.*;
import java.util.*;
import java.awt.*;
class THREADS extends GUI {
public static DigitalThreads
clock_thread = new DigitalThreads();
/** Draw all the shapes. */
synchronized public void paint(Graphics g) {
start_clock();
draw.grid(main_frame, g);
Geometry.compute_rays();
int numShapes = drawnShapes.size();
Shape s;
for (int i = 0; i < numShapes; i++) {
s = (Shape)drawnShapes.elementAt(i);
s.draw(g);
}
}
void start_clock() {
// note that the following will not work....
// clock_thread.g = g;
// Why not?
clock_thread.g = getGraphics();
clock_thread.f = main_frame;
clock_thread.start();
}
}
import java.util.*;
import java.awt.*;
import java.applet.Applet;
// DigitialThread must extend applet to getFontMetrics.
public class DigitalThreads extends Applet implements Runnable {
Thread runner;
Graphics g;
Frame f;
public void start() {
if (runner == null) {
runner = new Thread(this);
runner.start();
}
}
public void stop() {
if (runner != null) {
runner.stop();
runner = null;
}
}
synchronized private void draw() {
Dimension dim = f.size();
int height = dim.height - 60;
int width = dim.width;
Date theDate = new Date();
String date_string = theDate.toString();
int xloc = 10;
int yloc = dim.height - 60;
// g.setFont(f);
// get the string width in pixels this always returns 0.
int string_width = getFontMetrics(
g.getFont()).stringWidth(date_string);
int string_height = getFontMetrics(
g.getFont()).getHeight();
g.clearRect(xloc,yloc,string_width,string_height);
g.drawString(date_string, xloc,height+xloc);
}
public void run() {
while (true) {
draw();
try {Thread.sleep(1000);}
catch (InterruptedException e) {}
}
}
}
 Last Update:
04/09/97
Last Update:
04/09/97