CS411X - Lecture 10

Lecture Topic:

The Vector dot product
Determinants
2D Transformations
Basic Idea of Histogram
Sample Quiz

Matrix Addition

You add matrices which are of the same dimension by adding corresponding elements.

For example:

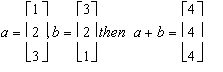
vectors add according to the parallelogram rule: to add the vectors v and w, take an arrow from the origin to w, translate it such that its base is at the point v, and define v+w as the new endpoint of the arrow:

The vector dot product

given two 2D vectors:

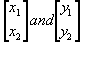
we compute the inner product or dot product as

this is denoted

In 3D:

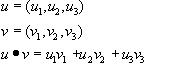
||v|| = magnitude of a vector == length of an n dimensional vector.

The distance between P and Q is the length of Q-P

Dot product properties

non degenerate : = v.v =0 iff v=0

bilinear : = v.(u + aw) = v.u + a(v.w)

Uses: dot products are good for normalizing a vector.

normalization:

a normalized vector has unit length

dot products are also good for finding the angle between vectors

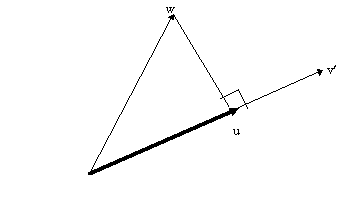
The projection of w onto the unit vector vÆ is a vector u. the length of u is ||w|| times the cosine of the angle between u and vÆ= q

arc = array element row# , col#

numbering starts at element 1

matrix multiplication

mxn * nxp = mxp

Determinants

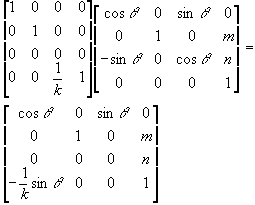
The determinant exists only for a square matrix for example:

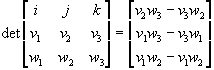
Cross Products

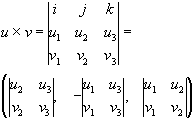
Dot products result in scalars. Cross products result in vectors. Two vectors are orthogonal if the dot product is zero. Prove that the cross product of two vectors results in an orthogonal vector i.e. u .(uxv) = 0

by definition.

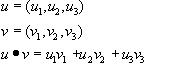
u .(uxv) = 0

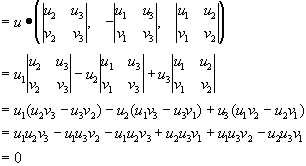
Q.E.D.

I will not make matrices bold as some books do. Also, my scalars will (often) have subscripts.

Transpose

transpose (nxm) = (mxn) for example:

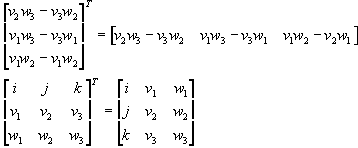
Matrix inversion

An inverse exists only if the matrix is square and the determinant is non zero.

You find the inverse by taking the transpose of the cofactors (adjoint) divided by the determinant.

From Hill, pp687: 1. Build a matrix of cofactors, C 2. Find |M| as the dot product of any row in C with a corresponding row of M 3. Transpose C and divide by |M|

For example :

2D Transformations

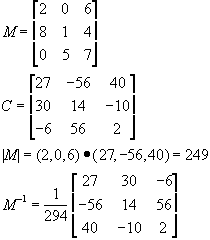
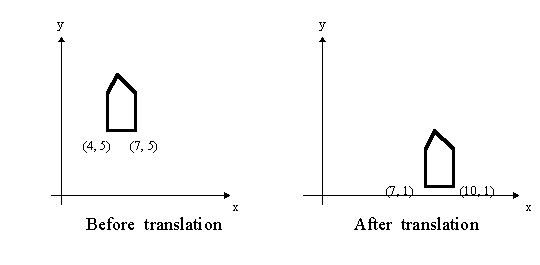
To translate a point on the (x,y) plane by adding translation amounts to the coordinates of the points:

In vector notation

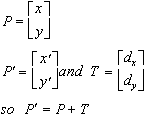
For example:

scaling

Points are scaled by multiplication:

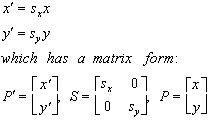
so that PÆ= SP

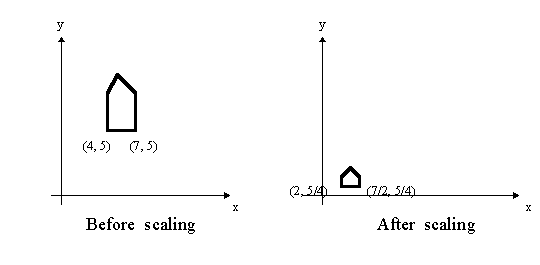
note that the house changes position, since the scaling is about the origin. If scaling were uniform, the amount of scaling in each dimension would be equal.

Rotation

An example of rotation about the origin

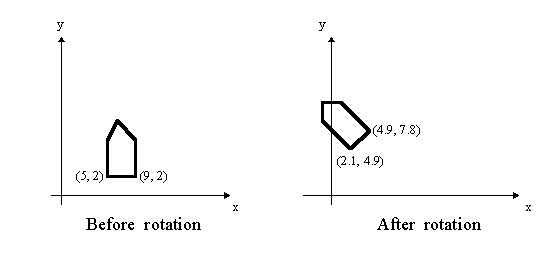
To rotate about another point, first translate the point to the origin, rotate, then translate back.

The following transforms perform rotation:

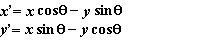
The angle of rotation is about the origin. Positive angles are measured counterclockwise. As an exercise, you should be able to reformulate the rotational transformations for negative angles. Use the identities:

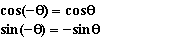
matrix formulation of the rotations:

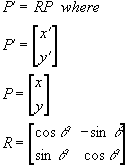
Proof:

Consider:

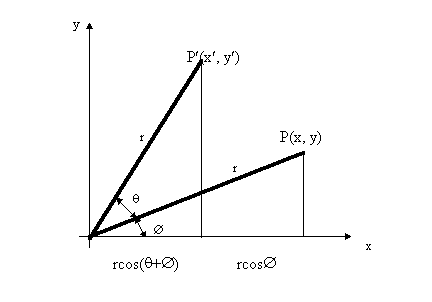
by simple trigonometry:

Basic Idea of Histogram

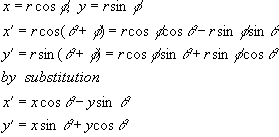
Chart showing PMF( Probably Miss Function )

PDF only for discrete systems.

** 2C

*** 3B

******* 7A

_______________________

P_G(A) = 7/12

P_G(B) = 3/12 =1/4

P_G(C) = 2/12 = 1/6

P_G(A) + P_G(B) + P_G(C) = 1

int I_A[] = new int[256];

int I_G[] = new int[256];

int I_R[] = new int[256];

int I_B[] = new int[256];

int R_I[] = new int[256];

for all Pixels

I_R(R) = I_R(R) + 1

I_G(G) = I_G(G) + 1

I_B(B) = I_B(B) + 1

I_A(A) = I_A(A) + 1

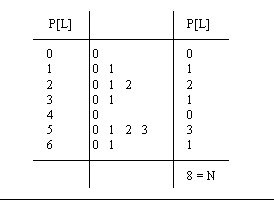
L = {2 3 5 1 2 5 5 6 }

for ( i = 1;à CARD[ L ] )

P[L] = P[L] + 1

int I_A[] = new double [256];

int I_G[] = new double [256];

int I_R[] = new double [256];

int I_B[] = new double [256];

L = { 2 3 4 1 2 5 5 6 }

for ( i = 1;à CARD[L] )

P[L] = P[L] +1;

for each elem

P[i] = P[i}/N

for each I in 255

P_i[i] = P_R(i) + P_G(i) + P_B(i) / 3

Sample Quiz

1. An Image Object can be get by