CS411X - Lecture 7

Lecture Topic:

Discrete Fourier Transform
Fast Fourier Transform
Danielson - Lanczos Lemma
Sample - Quiz

AudioFrame.java




import java.awt.*;
import java.io.*;
import sun.audio.*;
import java.applet.*;
        
public class AudioFrame extends Frame {
 
    private    Panel readoutPanel = new Panel();
 
    private     AudioStream audioStream;
    private            AudioDataStream audioDataStream;
 
    private     byte ulawData[] = null;
    private     double doubleData[] = null;
 
    AudioPlayer audioPlayer = AudioPlayer.player;
    private     String fileName;
    
    private     ObservableInt endPositionOfSamplesToGraph;
    private     ObservableInt startPositionOfSamplesToGraph;
    private final double pi_2 = Math.PI * 2;
    private final double pi = Math.PI;
    private final double samplingRate = 8000.0;
    private final double frequency = 440.0;
    
    private Scrollbar horizontalScrollbar;




int x-offset;
int w-size;




.
.
.




w-size = audioStream.getlength()-width -m -2;




    public void init_menu() {    
        // my menu items
        MenuBar menuBar = new MenuBar(); 
        // Initialize the menu bar
        setMenuBar(menuBar);
        menuBar.add(m);
        
        setBackground(Color.pink);
        //set title
        setTitle(fileName);
        horizontalScrollbar = new Scrollbar(Scrollbar.HORIZONTAL, 0, 20, 0, 25);
 
 
        add( "South", horizontalScrollbar);
 
        show();
    }
    
 
 public boolean handleEvent(Event e) {
    update();
 
        
        if (e.target == horizontalScrollbar) {
            switch (e.id) // more efficient, faster
                {
                    case e.SCROLL_ABSOLUTE:
                    case e.SCROLL_LINE_UP:
                    case e.SCROLL_LINE_DOWN:
                    case e.SCROLL_PAGE_UP:
                    case e.SCROLL_PAGE_DOWN:
                    repaint();
                }
 
            return true;
        }

Disk has an access time in m/s = 1* 10^-3

RAM has an access time in = 1*10^-9

In 2-D the DFT

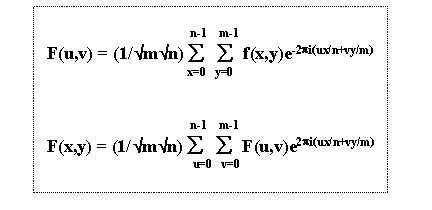
u, x = 0,Ö., n-1
x, y = 0,Ö., m-1

DFT input

f(x) output F(u)




complex[] DFT(double f[] ) {




N = f.length;
SQR_N = Math.SQRT(N);
double Pi2onN = 2*MathPi(N);
complex F[] = new complex [N];
for(u = 0; u<N; u++){




for(int x = 0; x<N; x++){




F[x].real = F[x].real + F[x]*cos(Pi2onN*x*u);
F[x].imaginary = F[x].imaginary + f[x]*sin(Pi2onN*x*u);




}
return F;

The DFT gives amplitude and Phase Harmonic at f_s / N Hz intervals.

The FFT require logN/log2 = log₂N

need a composite # of input samples.

N is typically a power of 2

Padding a sample with Oís alters the spectra.

In FFT we use divide and conquer, dividing up the sampling interval into subintervals.

Typically any length subinterval ( usually prime )

FFT may be performed iterative or recursively.

Danielson - Lanczos Lemma

Lemma: a DFT of length N can be written as the sum of 2

DFTís of length N/2 where N is a integer power of 2.

The first DFT is the even sample.

The second DFT is the odd sample.

Recall: DFT




m = 0,1Ö..N-1

call F(u), Fu and f(x), Fx




x = 0,1,2,3,Ö
2x = 0,2,4,Ö
2x+1 = 1,3,5,Ö.

Sample Quiz

1. Single Precison Data Type in Java is